Add & Norm（二）：从传统CV到Transformer里的Normalizaiton详解

1 写在前面

这一篇会稍微有点偏，我们要说明白Transformer中的LayerNorm和RMSNorm，需要把不同领域的Normalizaiton都过一遍。所以整个文章会从传统的CV领域的CNN开始说明，涉及不同数据样式、作用域和任务目标，最终说明Transformer中的LayerNorm和RMSNorm。

1.1 TL;DR

Normalization的核心目标是通过对数据进行变换，提升模型的训练稳定性、收敛速度和泛化能力。其本质是解决数据分布不一致、量纲差异或损失曲面不平滑等问题。不同领域因数据模态，比如图像、序列、时序信号等，和任务特性不同，演化出适配的 Normalization 技术。

对于传统CV，比如CNN，我们有BatchNorm、LayerNorm、InstanceNorm以及GroupNorm等。

对于NLP领域，尤其指我们在Transformer架构下，早期使用LayerNorm而现在通常使用RMSNorm，我们视为高效简化的LayerNorm。

2 Normalization的定义

\begin{aligned} μ & = \frac{1}{N} \sum_{i = 1}^{N} x_{i} \\ σ^{2} & = \frac{1}{N} \sum_{i = 1}^{N} (x_{i} - μ)^{2} \\ {\hat{x}}_{i} & = \frac{x_{i} - μ}{\sqrt{σ^{2} + ϵ}} \\ y_{i} & = γ {\hat{x}}_{i} + β \\ 其中： & N : 样本数量 \\ x_{i} : 第i个输入值 \\ μ : 均值 \\ σ^{2} : 方差 \\ {\hat{x}}_{i} : 归一化后的值 \\ γ : 可学习的缩放参数 \\ β : 可学习的偏移参数 \\ y_{i} : 仿射变换后的最终输出 \\ ϵ : 数值稳定性常数 \end{aligned}

Normalization的公式，除了最后的RMSNorm，我们接下来要说的BatchNorm、LayerNorm、IntanceNorm和GroupNrom都可以按照这个公式分为4步：

计算均值
计算方差
中心化
仿射变换

3 Norm的动机

深度神经网络训练过程中，中心协变量偏移（Internal Covariate Shift, ICS）曾被认为是阻碍收敛的关键因素。早期理论假设，通过Batch Normalization归一化各层输入的均值和方差，可消除ICS以加速优化。然而，目前学术界普遍接受的观点的是“损失平滑性是BN改善训练的主要原因”，BN提升训练效率的根本机制在于其对优化过程的重参数化（reparameterization），这种重构显著改善了损失函数的几何特性，平滑了损失曲面。

3.1 中心协变量偏移

中心协变量偏移（ICS） 是在深度神经网络训练过程中出现的一种现象。它指的是，随着网络参数（权重和偏置）在训练中不断更新，每一层网络的输入数据分布会发生变化。

虽然叫 “中心” ，其实翻译成 “内部” 更准确一些。它特指这种分布变化发生在神经网络的内部，而不是在模型的原始输入端。对于网络中的任何一层（比如第 L 层），它的输入是前一层（第 L-1 层）的输出。当第 L-1 层的参数更新时，它输出的数据的分布就会改变，从而导致第 L 层的输入分布也随之改变。

但是，ICS是影响神经网络训练收敛的阻碍，这一观点在2018年之后被改变了

3.2 平滑损失曲面

《How Does Batch Normalization Help Optimization?》 用了两个方法去证明ICS并非BatchNorm稳定训练的原因。

第一步，他们构建了一个带有BN的网络，正常训练，效果很好。然后，他们构建了一个“魔改”网络：在BN层之后，人为地注入随机的、不断变化的噪声来重新引入分布偏移。这意味着，网络的ICS问题依然严重。而即使ICS问题被人为地重新制造出来，这个网络的训练效果依然和标准BN网络一样好。

第二步，他们设计了多种“只稳定分布但不平滑曲面”的归一化方法，这些方法虽然成功抑制了ICS，但对训练的加速和稳定性几乎没有帮助。

所以他们提出，BN起作用的根本原因并非解决ICS问题，而是它对优化过程本身的重构，这导致了损失曲面的平滑。

那么什么是平滑损失曲面？

为了说明“平滑”，需要引入利普希茨性这一概念，它是一种数学定义上的平滑（放心，我们一会还会用说人话的方式去说明）。

其数学定义是，若存在常数 $L$ 使得函数 $f$ 对任意输入 $x_{1}, x_{2}$ 满足

∥ f (x_{1}) - f (x_{2}) ∥ \leq L \cdot ∥ x_{1} - x_{2} ∥

则称 $L$ 为函数的利普希茨常数（L-constant），表征函数变化的最大速率。

当 $L$ 较大时：损失曲面存在陡峭悬崖（Cliffs）或峡谷（Ravines），微小的参数移动可能导致损失值剧烈震荡。
当 $L$ 较小时：曲面呈平缓斜坡（Gentle Slopes），梯度方向稳定可预测。

说人话就是 我们通过梯度下降 去不断寻找一个最低点，或者说至少是一个足够低的“局部最小值”。但是其前提是，我们的下降都是平稳的。在一个整体平滑的山谷中，我们可以用梯度下降法去找。

但是，梯度通常找的是“最陡峭的下坡方向”。但是，梯度和人一样，如果前面是悬崖呢，只要往前一步，直接就会坠落，这就造成了梯度爆炸。又或者，我们所处的位置周围几乎是个平地，虽然在远处也许有下坡，但目前，我们就找不到下去的方向，这就造成了梯度消失。

所以，一个平滑的损失曲面就像一个平缓的山谷，在平缓的山谷中，优化算法每走一步，方向和大小都更具可预测性，不容易因为微小的移动就“飞出”好的区域。

平滑带来的好处包括：

允许使用更高的学习率： 在平滑的曲面上，你可以大胆地迈出更大步伐（高学习率）而不用担心“跑飞”。
加速收敛： 更高的学习率和更稳定的梯度方向自然导致训练速度更快。
更稳定的训练过程： 避免了梯度爆炸或消失的问题，使训练过程对初始化和超参数选择不那么敏感。

因此目前来说，更为被普遍接受的的理论是BN将一个原本崎岖、险峻的优化景观，“重塑”成一个更加平滑、易于探索的地形。

4 不同的领域的数据

在正式的说Normalization之前，我们必须先说一下不同领域的数据样式。因为不同的Normalization其实是其作用的数据形态不一样，这赋予了不同的现实意义，理解不同领域的数据样式有助于我们更好的理解。

4.1 传统CV下的数据样式

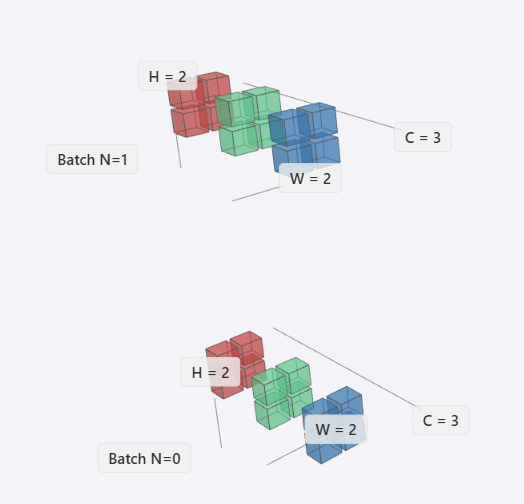
在传统CV领域下，在这里我们一般指CNN，会抽象为(N, C, H, W)四个维度。其中

N (Batch)：批大小，表示一次处理的图像数量。
C (Channels)：通道数，在视觉领域，我们将特征图的数量称为通道。比如RGB，就是三种颜色的通道。
H (Height)：图像高度，其垂直方向的像素数。
W (Width)：图像宽度，水平方向的像素数。
H 和 W 是两个完全独立的维度，分别表示空间上的垂直和水平方向。但这两个维度又是高度相关的，H x W构成了一个二维特征图，我们称为feature map。

我们可以把H×W看做一个平面，然后C是平面的堆叠。他们组成一个立方体之后，我们可以在这个立方体是堆叠Batch。

CNN的数据形态

这类数据具有空间结构，平移不变性，通道间存在相关性。

4.1.1 空间结构性

其实就是图像中的数据，我们说的最小单位，像素，它不是独立分布的。相邻的像素之间存在着强烈的相关性，也就是一个有意义的局部，比如一张图里画了只猫，这猫的耳朵，是多个像素组成的。

如果我们单独去看一个像素点，那它是灰色的、黑色、白色、还是其他任何颜色，它没有任何意义。但是观察它和周围的像素，这个特定的形状和纹理，就出来了。所以这个空间结构还具备两个特性：

局部性：图像中的基本特征，边缘、角点、纹理等，通常只依赖于一个很小的局部区域。一只眼睛的轮廓是由局部像素的颜色和亮度变化决定的，与图像另一角的尾巴无关。
层次性：简单的局部模式可以组合成更复杂的模式。
- 底层特征：几个像素点可以构成一条“边缘”或一个“角点”。
- 中层特征：几条边缘和角点在空间上以特定方式组合，可以构成“眼睛”或“鼻子”。
- 高层特征：眼睛、鼻子、耳朵等特征组合在一起，就构成了“猫脸”。

而CNN的核心，卷积就是空间结构思想的体现。这里不展开了，大概了解这个特点就好。

4.1.2 平移不变性

平移不变性（Translational Invariance) 的意思是，我们希望识别一个物体，无论它出现在图像的哪个位置。一只猫在图像的左上角和右下角都应该被识别为猫。而图的数据结构本身并没有这种特性，但是在CNN中，这个特性实际上是“平移等变性 (Translational Equivariance)”和“平移不变性 (Translational Invariance)”共同作用的结果。CNN的池化层和全局操作让特征可以被随处检测；将“等变性”逐步转化为“不变性”，让最终的识别结果不受位置影响。

4.1.3 通道相关性

对于通道相关性（Channel Correlation），其实非常符合我们的常识，我们可以从两个层面来理解，第一个是输入层，一般来说R、G、B三个颜色的通道，他们不是独立的。我们想要表示橙色，那就要需要高强度的R和中低强度的G和B。所以，从颜色角度，三个通道必然是相关的，只有一起才能编码“橙色”的颜色信息。

其次是中间特征图，我们可以把不同的中间通道看做一个特定类型的”特征检测器“，当我们有多个中间通道的时候，有的通道检测的是“橙色”，有的是检测“猫耳朵的边缘”，有的是“毛样的纹理”。所以这些通道的检测结果就有强烈的相关性。这些个特征图组合起来，很可能就是一个”橘猫“。

4.2 NLP下的数据样式

在NLP中则好想象的多，数据通常被抽象为三维张量 (B, S, D)，其中：

B (Batch)：批大小，表示一次处理的文本序列数量。这和视觉中的一次处理多张图片是同样的。
S (Sequence Length)：序列长度，表示每个文本的最大词元数量。对应图像里的H×W展平后的长度（这种说法只是为了方便我们理解两种领域的对应关系）。
D (Feature Dimension)：特征维度，表示每个词元的向量表示维度。对应图像里的channel数量。

NLP 数据的特点是序列长度可变（Variable-Length Sequences）。在处理同一批次中不同长度的序列时，通常需要通过填充（Padding）或截断（Truncation）对齐序列长度。模型输入的每个特征维度则共同编码文本的分布式语义表示，其中不同维度可能捕获语法、语义或上下文特征。

所以NLP数据的Feature Dimension虽然对应的是图像的Channel，但是相较Channel通常以RGB等颜色，Feature Dimension的特征维度需足够高，以支撑语义组合的复杂性。

4.3 NLP和CNN数据在空间上的转换

NCHW 到 (B, S, D) 的转换确实有多种方式，核心在于如何将图像的“空间维度”（H 和 W）以及“通道维度”（C）重新组织和解释为序列长度（S）和特征维度（D）。

CNN和NLP的数据形态对比

比如这张图，一种直观的转换思路是将图像的二维空间维度进行“展平”（Flattening）操作。具体而言，对于一个维度为 (N, C, H, W) 的图像张量，可以通过将高度（H）与宽度（W）维度直接相乘，将其重塑为一个长度为 H×W 的一维序列。例如，一个批次为2、通道为3、尺寸为2x2的图像 (2, 3, 2, 2)，通过展平可转换为 (2, 4, 3) 的序列化张量，其中序列长度S为4，特征维度D为3。

直接把H和W相乘，真的可以这样做么？

展平操作的核心问题在于它粗暴地破坏了图像固有的二维空间局部性。在原始的图像网格中，一个像素与其上下左右的邻近像素在语义上具有强相关性，这种空间邻接关系是图像理解，比如边缘检测、纹理识别的基础。然而，在展平后的线性序列中，原本垂直相邻的两个像素，比如坐标(x, y)与(x, y+1)的像素，可能会在序列中相距甚远，其空间关联性被完全消除。这种信息损失是巨大的，它使得模型无法有效学习到基于空间位置的视觉模式，从而严重制约了模型性能的上限，尤其是在需要精细空间推理的复杂视觉任务中。

于是我们有了ViT（Vision in Transformer）。ViT是现代的CV架构，其逻辑是不在将单个像素视为序列单元，而是将图像分割成一系列不重叠的、固定大小的图像块（Patches）。例如，一张224x224的图像可以被分割成196个16x16的图像块。每一个图像块作为一个整体，保留了其内部的局部二维结构。这一“分块化”（Patching）策略。它在宏观上将图像问题转化为序列问题，同时在微观上维持了关键的局部空间信息。

这里不深入展开ViT，主要是为了理解传统CV和NLP的数据形态对应关系。尽管这种转换方式存在一定问题，最终引导到ViT这一适合视觉和自然语言的模型。

5 Normalization

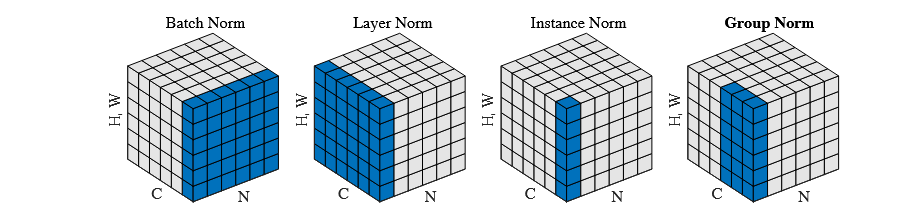
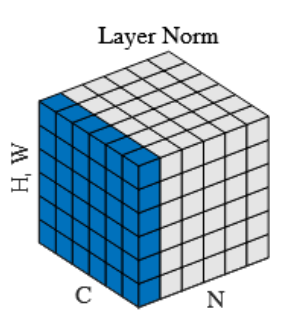
现在，我们有了足够的前置知识，可以开始说说Normalization了。这张图出自Group Normalization，网上特别多。不过该图是说明了CNN中应用的4种Normalization方法。其中LayerNorm是我们要讲的主要情况，不过需要注意的是，CNN中的LayerNorm和NLP的概念一样，但是因为数据形态和应用领域原因，作用域不同。所以我们先从CNN开始说。

CNN中的四种Norm

5.1 CNN中的Norm

5.1.1 Batch Norm

BatchNorm

BatchNorm作为开创性的工作，是我们不得不提到的一个Nomalization，它主要是应用在计算机视觉的CNN中。在NLP或者音频领域，则不被推荐。

5.1.1.1 定义

Batch Normalization 指的是逐通道计算每个通道在整个当前 Batch （mini-batch）和所有空间位置上的均值和方差，并使用这些统计量对该通道的所有激活值进行归一化，最后应用一个逐通道的仿射变换。

5.1.1.2 公式

\begin{aligned} μ_{c} & = \frac{1}{N \cdot H \cdot W} \sum_{n = 1}^{N} \sum_{h = 1}^{H} \sum_{w = 1}^{W} x_{n, c, h, w} \\ σ_{c}^{2} & = \frac{1}{N \cdot H \cdot W} \sum_{n = 1}^{N} \sum_{h = 1}^{H} \sum_{w = 1}^{W} (x_{n, c, h, w} - μ_{c})^{2} \\ {\hat{x}}_{n, c, h, w} & = \frac{x_{n, c, h, w} - μ_{c}}{\sqrt{σ_{c}^{2} + ϵ}} \\ y_{n, c, h, w} & = γ_{c} {\hat{x}}_{n, c, h, w} + β_{c} \\ 其中： & N : Batch size，批次大小 \\ H : Height，特征图高度 \\ W : Width，特征图宽度 \\ C : Channels，通道数 \\ x_{n, c, h, w} : 输入张量 \\ μ_{c} : 第c个通道的均值 \\ σ_{c}^{2} : 第c个通道的方差 \\ {\hat{x}}_{n, c, h, w} : 归一化后的值 \\ γ_{c}, β_{c} : 可学习的缩放和偏移参数 \\ ϵ : 数值稳定性常数 \\ y_{n, c, h, w} : 最终输出 \end{aligned}

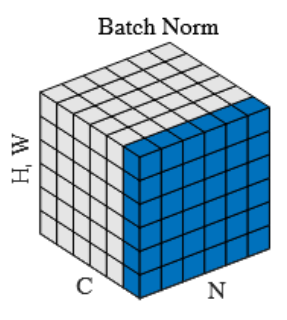
5.1.1.3 BN示意图

BN的操作从图中，可以理解为沿着Channel的数量，有多少个channel，我们就沿着channel切n-1下，分割出来的每个channel下所有的 N x W x H个元素进行归一化。在torch中就是dim1。

BatchNorm in CNN

5.1.1.4 理解BatchNorm的隐式表达

我们来认真分析一下这个公式背后所代表的意义。

BatchNorm不在乎单个图的单个channel的特点，它要的是，这一个mini-batch下，多个样本（图），在同一个channel中的统一的共性或者标准。

怎么去理解呢？这里有两个关键点：

数据特征：图像数据的通道具有先天结构一致性：同一批次内所有样本的通道数量，一个批次内的所有图像样本N在结构上是高度对齐的，它们共享相同的空间维度（H×W）与通道数量（C）。这使得跨样本的通道统计量（ $μ_{c}, σ_{c}$ ）具备可比性。
通道语义：特定通道在语义上具有一致性。该通道的激活图代表了网络中特定卷积核对所有输入图像提取出的同一种模式或特征，例如边缘、纹理或特定物体的部件。因此，BN将不同图像的同名通道，比如R通道，视作一个统计整体，其本质是同通道特征应服从统一分布。

那问题来了，多个channel的数据一起进行归一化，不就被破坏了原本数据提供的信息吗？

5.1.1.5 仿射变换

所以我们就要提一下仿射变换。其实之前我们也提到过仿射变换，在FFN中，我们用的是线性和非线性，其实，在深度学习这一语境下，在FFN中的“线性层”，它通常指代仿射变换。

线性是有中心不变性，也就是说不会有偏置项。而仿射则是我们常见的 $y = a x + b$ 的形式。
在严格的数学定义下：

仿射变换（Affine）： $y = a x + b$
纯线性变换（Linear）： $y = a x$

那么仿射变换在BatchNorm中有什么用呢？

他给予了模型一定程度上恢复原有分布的能力，也就是说，通过Norm去平滑损失曲面的同时，还获得了可控的恢复能力。

BatchNorm数据不同阶段

那为什么Batch数量不够，Batch Norm就效果不好了？

其实回顾我们之前说的BN的思想本质：

BatchNorm不在乎单个图的单个channel的特点，它要的是，这一个mini-batch下，多个图，在同一个channel中的统一的共性或者标准。

当批量大小（N）充足时，批次内包含了足够多样化的样本，其计算出的均值和方差能够可靠地代表该特征在全局数据上的“共性标准”。然而，当N急剧缩小时，这个统计基础便开始瓦解。一个仅包含少数几个样本的批次，其计算出的“共性”很可能是充满偏差和噪声的“伪共性”。比如，如果一个批次恰好只包含两张昏暗场景的图像，那么BN会错误地将“昏暗”作为所有特征的“标准”进行归一化。那么可以说，这次的样本是无法代表全局分布的。

我们拿一个极端的例子，那就是N=1的时候，那么BatchNorm所要找的“共性”则不存在，因为某个channel下，它只有自己本身可以去参照，而没有跨多个样本，找到多个图片某个的共同特征的能力。BN操作退化为一种“自我参照”式的变换，这在数学上等同于实例归一化（Instance Normalization）。

所以BatchNorm通常不能在NLP上用的原因是什么？

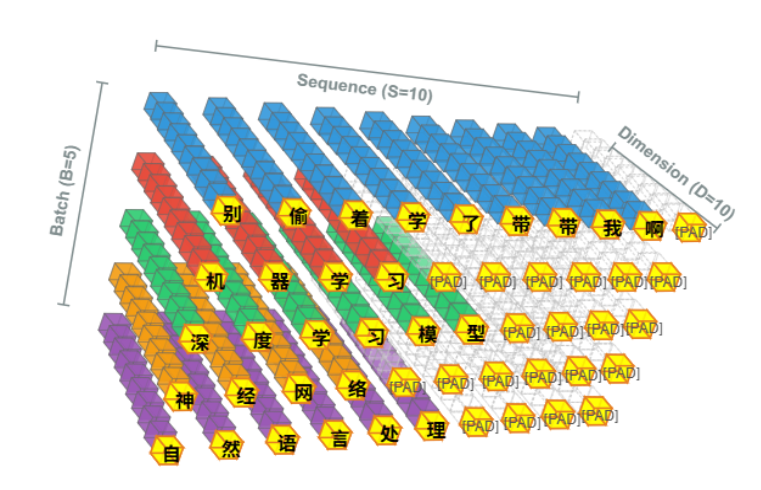
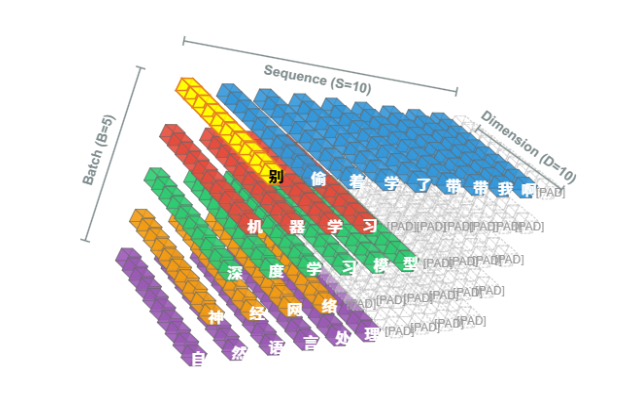
用图说一下BatchNorm破坏文本语义的特点。比如我们有一个batch size为5的embedding后的数据，其feature dimension为10。如果我们对它进行BatchNorm会发什么？

在NLP上强行套用BN的效果

图中黄色部分是我们BatchNorm应用对象。首先，所有的句子因为长度不同需要进行填充，所以我们有大量的<PAD>符号，这种符号相当于在有意义的数据中加入了大量假信息，从而污染了整个BN的作用域。

其次是语义位置的敏感性，同一个特征通道，在NLP场景下，是feature dimension的位置。每个词嵌入向量的分量位置，理论上应编码特定语义属性，比如如词性或上下文关系，由于语言本身的多样性，同一维度位置在不同词汇中可能承载截然不同的含义。比如“学”的第一个dimension和“型”的第一个dimension，因为词的语义天然是两种，动词和名词，所以他们位置含义无法被统一。

标准NLP模型中的词嵌入是**分布式表示（Distributed Representation）**。这意味着：

一个词的完整语义并不是由某个单一维度来编码的，而是通过整个向量空间中所有维度的复杂组合来表达的。意义蕴含在向量的方向和与其他向量的关系中，而非单个维度的数值。

单个维度通常不具备独立、可解释的含义。第 d 维可能同时参与编码一个词的语法属性、情感色彩、所属领域等多种信息，并且这种编码方式对于不同词是不同的。我们无法轻易地给第 d 维贴上一个“情感极性”或“物体大小”的标签。

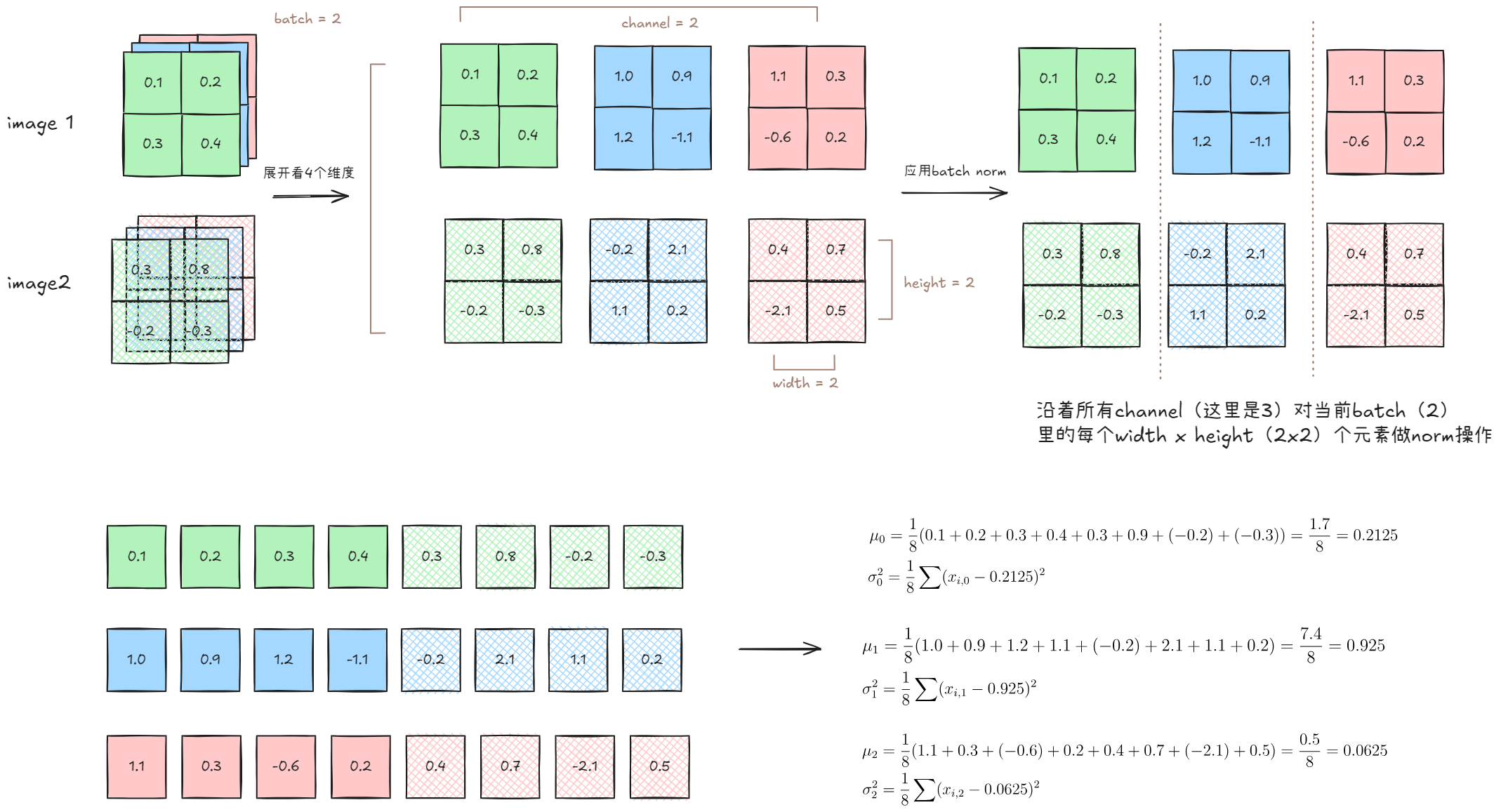
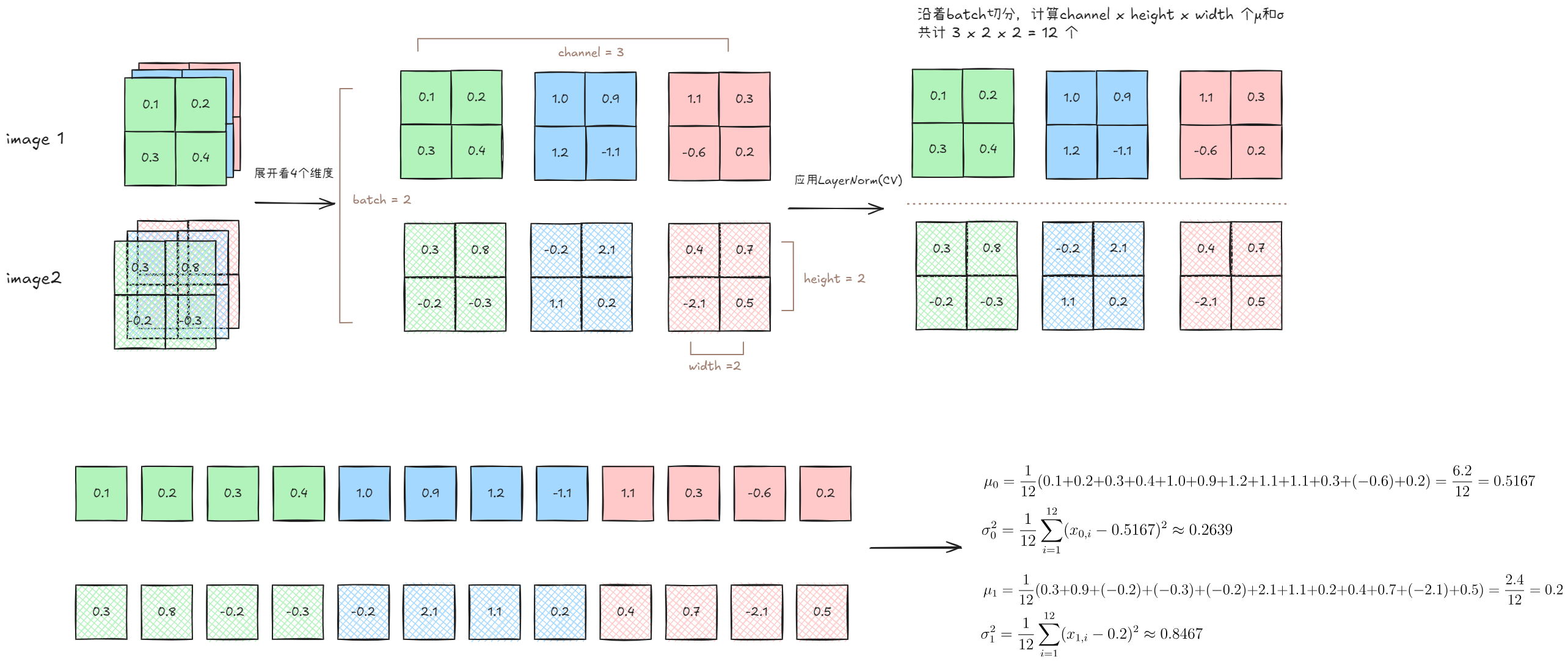
5.1.1.6 对比torch实现和手动实现BN

假设我们的两组数据如下：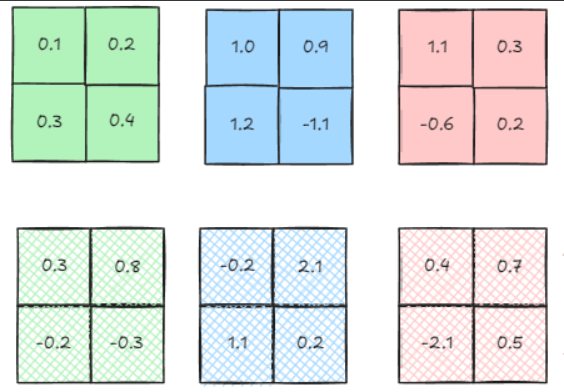
batch size为2的数据

使用torch.nn.BatchNorm2d

python

import torch
import torch.nn as nn

# 设置tensor显示选项，避免科学计数法
torch.set_printoptions(precision=6, sci_mode=False)

# 创建数据张量
data = torch.tensor([
    [  # Batch 0
        [[0.1, 0.2], [0.3, 0.4]],      # Channel 0 (绿色)
        [[1.0, 0.9], [1.2, -1.1]],     # Channel 1 (蓝色)
        [[1.1, 0.3], [-0.6, 0.2]]      # Channel 2 (粉色)
    ],
    [  # Batch 1
        [[0.3, 0.8], [-0.2, -0.3]],    # Channel 0 (绿色)
        [[-0.2, 2.1], [1.1, 0.2]],     # Channel 1 (蓝色)
        [[0.4, 0.7], [-2.1, 0.5]]      # Channel 2 (粉色)
    ]
], dtype=torch.float32)

# PyTorch BatchNorm计算
batch_norm = nn.BatchNorm2d(num_features=3)
batch_norm.train()
torch_result = batch_norm(data)

for i in range(3):
    print(f"\n{'='*20} Channel {i} {'='*20}")
    print("PyTorch结果:")
    print(torch_result[:, i, :, :])

手动计算

python

input_tensor = data
N, C, H, W = input_tensor.shape
output = torch.zeros_like(input_tensor)

for c in range(C):
    print(f"[CHANNEL {c}]:")
    channel_data = input_tensor[:, c, :, :]
    mean = channel_data.mean()
    print(f"[ORIGINAL CHANNEL DATA]:\n{channel_data}")
    print(f"mean is {mean}")
    print(f"var is {channel_data.var(unbiased=False)}")
    print("-"*50)
    normalized = (channel_data - mean) / torch.sqrt(channel_data.var(unbiased=False) + batch_norm.eps)
    print(f"[MANUAL NORMALIZED]:\n{normalized}")
    output[:, c, :, :] = normalized
    print("-"*50)
    print(f"[TORCH NORMALIZED]:")
    print(torch_result[:, c, :, :])
    print("="*50)

得到的对比结果：

python

[CHANNEL 0]:
[ORIGINAL CHANNEL DATA]:
tensor([[[ 0.100000,  0.200000],
         [ 0.300000,  0.400000]],

        [[ 0.300000,  0.800000],
         [-0.200000, -0.300000]]])
mean is 0.20000000298023224
var is 0.10500000417232513
--------------------------------------------------
[MANUAL NORMALIZED]:
tensor([[[-0.308592,  0.000000],
         [ 0.308592,  0.617184]],

        [[ 0.308592,  1.851552],
         [-1.234368, -1.542960]]])
--------------------------------------------------
[TORCH NORMALIZED]:
tensor([[[    -0.308592,     -0.000000],
         [     0.308592,      0.617184]],

        [[     0.308592,      1.851552],
         [    -1.234368,     -1.542960]]], grad_fn=<SliceBackward0>)
==================================================
[CHANNEL 1]:
[ORIGINAL CHANNEL DATA]:
tensor([[[ 1.000000,  0.900000],
         [ 1.200000, -1.100000]],

        [[-0.200000,  2.100000],
         [ 1.100000,  0.200000]]])
mean is 0.6499999761581421
var is 0.8474999666213989
--------------------------------------------------
[MANUAL NORMALIZED]:
tensor([[[ 0.380186,  0.271561],
         [ 0.597435, -1.900928]],

        [[-0.923308,  1.575055],
         [ 0.488810, -0.488810]]])
--------------------------------------------------
[TORCH NORMALIZED]:
tensor([[[ 0.380186,  0.271561],
         [ 0.597435, -1.900928]],

        [[-0.923308,  1.575054],
         [ 0.488810, -0.488810]]], grad_fn=<SliceBackward0>)
==================================================
[CHANNEL 2]:
[ORIGINAL CHANNEL DATA]:
tensor([[[ 1.100000,  0.300000],
         [-0.600000,  0.200000]],

        [[ 0.400000,  0.700000],
         [-2.100000,  0.500000]]])
mean is 0.06250002980232239
var is 0.8723437190055847
--------------------------------------------------
[MANUAL NORMALIZED]:
tensor([[[ 1.110815,  0.254283],
         [-0.709316,  0.147216]],

        [[ 0.361349,  0.682549],
         [-2.315313,  0.468416]]])
--------------------------------------------------
[TORCH NORMALIZED]:
tensor([[[ 1.110815,  0.254283],
         [-0.709316,  0.147216]],

        [[ 0.361350,  0.682549],
         [-2.315314,  0.468416]]], grad_fn=<SliceBackward0>)
==================================================

5.1.2 Layer Norm

CNN中的LayerNorm

5.1.2.1 定义

Layer Normalization的提出，是在理解BN的基础上进行的，因BN依赖批次大小而受限的场景，提出LN。

首先我们理解LN的操作。CNN中的LN针对单个训练样本，计算其所有特征维度上的均值和方差，并使用这些专属于该样本的统计量，对其所有特征进行归一化，最后应用一个逐元素的仿射变换。这种归一化机制的核心在于其计算完全在单个样本内部完成，不依赖于批次中的任何其他样本。

5.1.2.2 公式

\begin{aligned} μ_{n} & = \frac{1}{C \cdot H \cdot W} \sum_{c = 1}^{C} \sum_{h = 1}^{H} \sum_{w = 1}^{W} x_{n, c, h, w} \\ σ_{n}^{2} & = \frac{1}{C \cdot H \cdot W} \sum_{c = 1}^{C} \sum_{h = 1}^{H} \sum_{w = 1}^{W} (x_{n, c, h, w} - μ_{n})^{2} \\ {\hat{x}}_{n, c, h, w} & = \frac{x_{n, c, h, w} - μ_{n}}{\sqrt{σ_{n}^{2} + ϵ}} \\ y_{n, c, h, w} & = γ {\hat{x}}_{n, c, h, w} + β \\ 其中： & N : Batch size批次大小 \\ C : Channels，通道数 \\ H : Height，特征图高度 \\ W : Width，特征图宽度 \\ x_{n, c, h, w} : 输入张量 \\ μ_{n} : 第n个样本的均值 \\ σ_{n}^{2} : 第n个样本的方差 \\ {\hat{x}}_{n, c, h, w} : 归一化后的值 \\ γ : 可学习的缩放参数 \\ β : 可学习的偏移参数 \\ y_{n, c, h, w} : 仿射变换后的最终输出 \\ ϵ : 数值稳定性常数 \end{aligned}

5.1.2.3 CNN-LN示例图

CNN下的LN，是沿着Batch切分，将一个样本中的所有的C、H、W的每一个元素都放在一起进行归一化。可以理解为，当batch size是n，我们就沿着batch size横着切n-1下。如果batch size是2，那只要一下。计算方式如下图：

LayerNorm in CNN

5.1.2.4 理解CNN-LN的隐式表达

其实LayerNorm的提出动机就是为了解决BatchNorm对batch size的依赖。其思想就是不依赖批次的结构，而是在单个样本的所有特征维度上计算均值和方差。这意味着，无论输入是图像（C×H×W）、序列（S×D），还是任意高维张量，LN都将其展平为一组特征，并在这些维度上进行归一化。

这种Norm方式隐含了一个假设：一个样本的不同特征维度，不论是词向量的不同分量或者图像的不同通道，应当在统计上保持某种平衡。

LayerNorm效果不好？现代CV已经不在使用这种LayerNorm？

CNN 的一个核心假设是通道之间承载着相对独立的、专门化的特征。例如，一个通道可能用于检测垂直边缘，另一个通道用于检测红色斑块。它们的激活值和统计分布本身就是有意义的。LN 强行将这些功能迥异的通道拉到一起进行归一化，破坏了它们各自独立的统计信息，损害了模型的表征能力。 这才是 LN 在 CNN 中表现不佳的关键原因。声明中提到的“相对性”和“分布式的值”虽然直觉上指向了这个问题，但未能准确表达出“破坏通道独立性假设”这一核心学术概念。

所以在论文中所提及的，LayerNorm其实并不适合传统的CNN任务，它的效果并无法和BatchNorm分庭抗礼。因为LayerNorm对模型表征能力的损害，使得其上限并不高。

5.1.3 InstanceNorm

InstancceNorm

5.1.3.1 定义

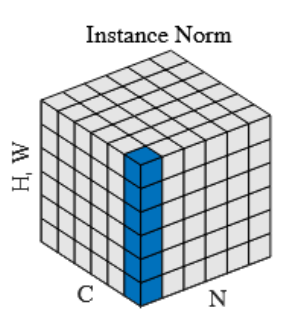
相较之下，Instance Normalization是对一个样本的一个通道的空间维度H x W进行归一化，进行Batch x Channel次数。这样每个的每个通道都对自己做了归一化。在给定样本的特定通道c上，IN仅基于该通道所有空间位置（H×W个像素点）计算均值与方差。

5.1.3.2 公式

\begin{aligned} μ_{n, c} & = \frac{1}{H \cdot W} \sum_{h = 1}^{H} \sum_{w = 1}^{W} x_{n, c, h, w} \\ σ_{n, c}^{2} & = \frac{1}{H \cdot W} \sum_{h = 1}^{H} \sum_{w = 1}^{W} (x_{n, c, h, w} - μ_{n, c})^{2} \\ {\hat{x}}_{n, c, h, w} & = \frac{x_{n, c, h, w} - μ_{n, c}}{\sqrt{σ_{n, c}^{2} + ϵ}} \\ y_{n, c, h, w} & = γ_{c} {\hat{x}}_{n, c, h, w} + β_{c} \\ 其中： & N : Batch size（批次大小） \\ C : Channels（通道数） \\ H : Height（特征图高度） \\ W : Width（特征图宽度） \\ x_{n, c, h, w} : 输入张量 \\ μ_{n, c} : 第n个样本第c个通道的均值 \\ σ_{n, c}^{2} : 第n个样本第c个通道的方差 \\ {\hat{x}}_{n, c, h, w} : 归一化后的值 \\ γ_{c} : 第c个通道的可学习缩放参数 \\ β_{c} : 第c个通道的可学习偏移参数 \\ y_{n, c, h, w} : 仿射变换后的最终输出 \\ ϵ : 数值稳定性常数 \end{aligned}

5.1.3.3 理解IN的隐式表达

其隐式表达是：

样本之间独立，因为我们没有跨样本
通道之间独立，因为我们也没有跨通道
空间维度归一化：我们只在 H x W维度上计算
这进一步得出，它消除了每个通道内的统计偏差，保持了不同通道的相对关系。所以我们可以理解为，我们把不同的通道的风格移除，比如把颜色移除了，我们可以重新上色，图还是那个图，但是颜色风格已经变了。（当然，通道不完全等同于颜色，还有其他特征）

这种设计剥离了样本间的统计依赖，突显单幅图像内部的风格特征。机制上，IN通过消除样本特有的光照、对比度等全局风格差异，使模型聚焦于局部结构信息。 这种特性在风格迁移任务中被证实具有独特优势——生成图像的风格描述子（如纹理、笔触）主要依赖于单幅图像内部的统计特征。

5.1.4 Group Norm/Power Norm

GroupNorm

5.1.4.1 定义

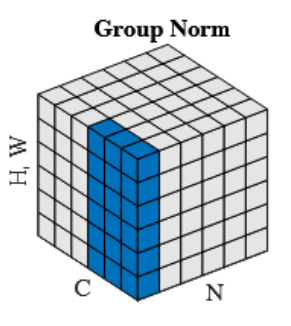
组归一化（Group Normalization, GN）的提出，是在理解BN、IN和LN各自局限性的基础上进行的。BN依赖批次大小而在小batch场景下不稳定；IN完全独立处理每个通道，统计信息过于稀疏；LN对所有通道统一归一化，可能混合语义差异巨大的通道特征。GN提出了一种介于IN和LN之间的折中方案。

首先我们理解GN的操作。GN针对单个训练样本，将其通道维度按索引顺序机械地划分为若干个组（group），计算每个组内所有通道在空间维度上的均值和方差，并使用这些专属于该样本该组的统计量，对组内所有通道进行归一化，最后应用一个逐通道的仿射变换。这种归一化机制的核心在于其计算完全在单个样本内部的通道组中完成，既不依赖于批次中的其他样本，也避免了IN的统计信息稀疏问题和LN的特征混合问题。

5.1.4.2 公式

\begin{aligned} μ_{n, g} & = \frac{1}{(C / G) \cdot H \cdot W} \sum_{c = g \cdot C / G}^{(g + 1) \cdot C / G - 1} \sum_{h = 1}^{H} \sum_{w = 1}^{W} x_{n, c, h, w} \\ σ_{n, g}^{2} & = \frac{1}{(C / G) \cdot H \cdot W} \sum_{c = g \cdot C / G}^{(g + 1) \cdot C / G - 1} \sum_{h = 1}^{H} \sum_{w = 1}^{W} (x_{n, c, h, w} - μ_{n, g})^{2} \\ {\hat{x}}_{n, c, h, w} & = \frac{x_{n, c, h, w} - μ_{n, g}}{\sqrt{σ_{n, g}^{2} + ϵ}} \\ y_{n, c, h, w} & = γ_{g} {\hat{x}}_{n, c, h, w} + β_{g} 其中： \\ q u a d & N : Batch size（批次大小） \\ C : Channels（通道数） \\ H : Height（特征图高度） \\ W : Width（特征图宽度） \\ G : Groups（组数） \\ g : 组的索引, g \in 0, 1, \dots, G - 1 \\ x_{n, c, h, w} : 输入张量 \\ μ_{n, g} : 第n个样本第g组的均值 \\ σ_{n, g}^{2} : 第n个样本第g组的方差 \\ {\hat{x}}_{n, c, h, w} : 归一化后的值 \\ γ_{g} : 第g组的可学习缩放参数 \\ β_{g} : 第g组的可学习偏移参数 \\ y_{n, c, h, w} : 仿射变换后的最终输出 \\ ϵ : 数值稳定性常数 \end{aligned}

5.1.4.3 理解GN的隐式表达

在CNN中，GN构建了一个统计信息丰富度的连续谱系：

GN通过设置不同的组数量，可以在IN（每组1个通道）和LN（1组包含所有通道）之间连续调节。分组策略是完全机械的：将通道按索引顺序均匀分配到各组中，而非基于语义相关性。尽管这种分组方式看似粗糙，但在实践中却表现出良好的效果，这可能是因为相邻通道在训练过程中往往会自然学习到相关的特征模式。

与其他归一化方法相比，GN在统计信息的丰富性和特征独立性之间找到了经验上有效的平衡点：比IN拥有更丰富的统计信息（多通道联合），比LN具有更好的特征独立性（避免无关通道混合），同时完全摆脱了BN对批次大小的依赖。这使得GN在目标检测、语义分割等对batch size敏感的任务中表现出更强的鲁棒性和稳定性。

那GN不就是分割的LN么？为什么LN就不好，GN就好了？

LN的做法是，对于一张输入的图片，将所有通道的特征“一视同仁”，把它们全部混合在一起计算一个统一的均值和方差来进行归一化。这种操作带来一个严重问题：它错误地假设了所有通道的特征在统计上是相似且应该被同等对待的。

实际上，猫眼特征的数值分布和背景草地的数值分布可能天差地别。强行将它们归一化，会削弱各自特征的独特性。

GN承认了不同通道间的巨大差异，但又不像实例归一化（IN）那样完全放弃通道间的关联。它的核心思想是：虽然所有通道不能一概而论，但功能相近的通道可以放在一起考虑。

GN的“分割”操作，就是基于一个非常合理的工程假设：在CNN的训练过程中，网络倾向于将功能相似的卷积核（即通道）组织在一起。 也就是说，负责检测边缘的通道们，它们的索引号可能更接近；负责识别纹理的通道们，也可能被安排在相邻的位置。

6 看了这么多，Normalization的本质是？

仔细观察上面的Norm，不同的normalization方法的公式没有怎么变，唯一改变的是他们作用的对象或者范围不同。为什么就效果就不一样了？

作用域和隐式表达。 作用域和隐式表达。 作用域和隐式表达。

是的，作用域就是这么重要。

对比多个Norm，他们本质方法并没有改动。不同Norm的根源在于它们各自的作用域（normalization scope） 赋予了其独特的归纳偏置（inductive bias）** 或者说隐式表达。在我们上面看的CNN领域下：

Batch Normalization (BN) 表示的是：在一个批次内，对每个特征通道独立地计算均值和方差。这意味着，对单个样本的归一化，其统计量来自于同一批次内的所有其他样本。这种跨样本的统计依赖，使得模型隐式地利用了批次内的信息分布，起到了正则化效果，但也导致了其性能严重依赖批次大小。
Layer Normalization (LN) 表示的是：在单个样本内部，对所有通道/特征维度进行归一化。这确保了每个样本的计算完全独立于批次中的其他样本。但LN假设了所有通道都服从同一分布，而这一假设在CNN中并不符合逻辑导致其效果在CNN中并不好。
Instance Normalization (IN) 将独立性推向极致，它在单个样本的单个通道内部进行归一化。这种操作的隐式特性是 “内容与风格的分离”。通过移除每个特征通道自身的均值和方差（即对比度、亮度等风格化统计信息），IN能有效剥离原始图像的风格，使模型聚焦于空间结构（内容），因此在图像风格迁移任务中取得了巨大成功。
Group Normalization (GN) 是介于LN和IN之间的灵活折中。它将通道分成若干组，在组内进行归一化。其隐式表达是：特征通道并非完全独立（如IN）或完全同质（如LN），而是存在功能相关的“特征群组”。GN在维持群组内部统计依赖的同时，隔离了不同群组间的干扰。这使其既能摆脱批次依赖，又比LN保留了更多结构化的特征信息，因而在目标检测、分割等视觉任务中表现稳定且出色。

理解不同Norm的关键，不在于硬背他做了什么。而是理解其作用域，因为作用域的现实意义反应了Norm操作的隐式表达。这也就是为什么在讲Norm之前，我们不得不花大量的篇幅去说明不同类型的数据样式的特点。因为他们才是Norm操作含义的根本原因。

到这里，我们终于可以展开的Transformer中的Normalization了。因为我们已经充分说明了不同任务下的数据特征带来的操作意义不同。也明白了，Normalization的作用域不同所带来的一些隐式含义。那么在Transformer中应用LayerNorm就很好理解了。

7 在Transformer中的Normalization

7.1 LayerNorm

LayerNorm的公式还是和之前一样，不过这次我们简化一下来看。

LayerNorm (x) = γ ⊙ \frac{x - μ}{\sqrt{σ^{2} + ϵ}} + β

7.1.1 数据形态及其特点

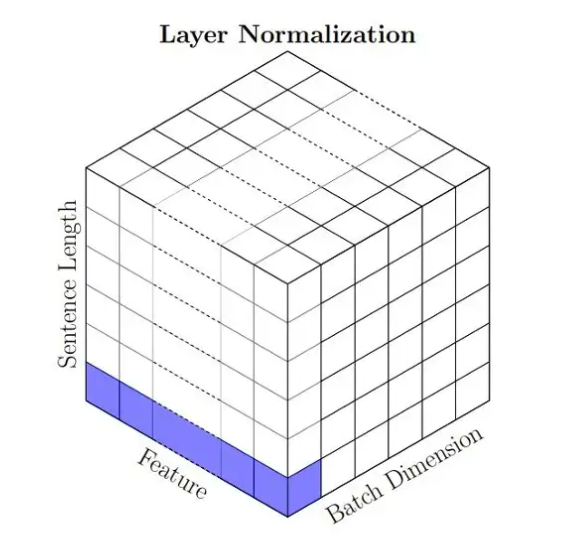
LayerNorm in Transformer

为什么LayerNorm在NLP里和传统CV里是不一样的？这里怎么是一个“条”，而CNN里是一个“面”

这LayerNorm既然是个“条”不就是IntanceNorm？

7.1.2 “层”概念的不同

第一个问题的本质是不同架构的层概念不同。

先前说过CNN中的LayerNorm是对Batch下的单个样本的所有Channel的H x W一起进行归一化。

而换到NLP中，根据Channel对应Feature Dimension，而Sequence Length则代表H x W，如果想CNN中对整个Sequence Length上的所有Feature Dimension都进行归一化，其隐式表达就会是理解成一个sequence上的每个token应该有类似的分布。

这种分布的异质性源于语言的多层结构特性。从语义层面看，主语与宾语承担不同的语法角色，其上下文依赖模式呈现非对称性；从语用层面看，句首的引导词（比如“比如”）与句尾的结论词（比如"所以"）承载截然不同的语篇功能。计算语言学实验证实，即使在同一语义场景下，不同词性的token也存在差异，这种差异在注意力机制中会被几何级放大。

所以LayerNorm 的核心原理始终没变，只是它作用的‘层’的形态不同。

我们要再次强调Transformer架构的数据形式是三维，B x S x D。而传统CV下，数据形式是四维的，B x C x H x W。

那么在 Transformer 中，‘层’是一个个独立的词向量，所以 LN 独立作用于每个词向量的特征上。在 CNN 中，‘层’是整个三维的特征图（C x H x W），所以理论上 LN 会作用于整个特征图。

如果我们再换到之前提到过的ViT，也就是现代的CV，其 LayerNorm 和 NLP 中的用法是完全一样的，因为它们都把数据处理成了序列。所以，差异本身是模型架构对数据格式的抽象定义不同导致的。其概念始终如一。

7.1.3 Transformer中的LayerNorm的可视化

LayerNorm的实际应用示例

还是这个图，黄色部分是我们的LayerNorm的作用域，可以看出来，它是对一个词本身的feature dimension进行归一化，然后执行BatchSize x Sequence Length次，在这里就是 $5 * 10 = 50$ 次。

这里可以直观的看出其在可变文本领域的优势，由于每个词元的归一化统计量完全在其自身的特征维度上计算，一个序列中真实词元的归一化计算不会受到另一序列中PAD词元统计特征的干扰

7.1.4 LayerNorm和InstanceNorm的区别

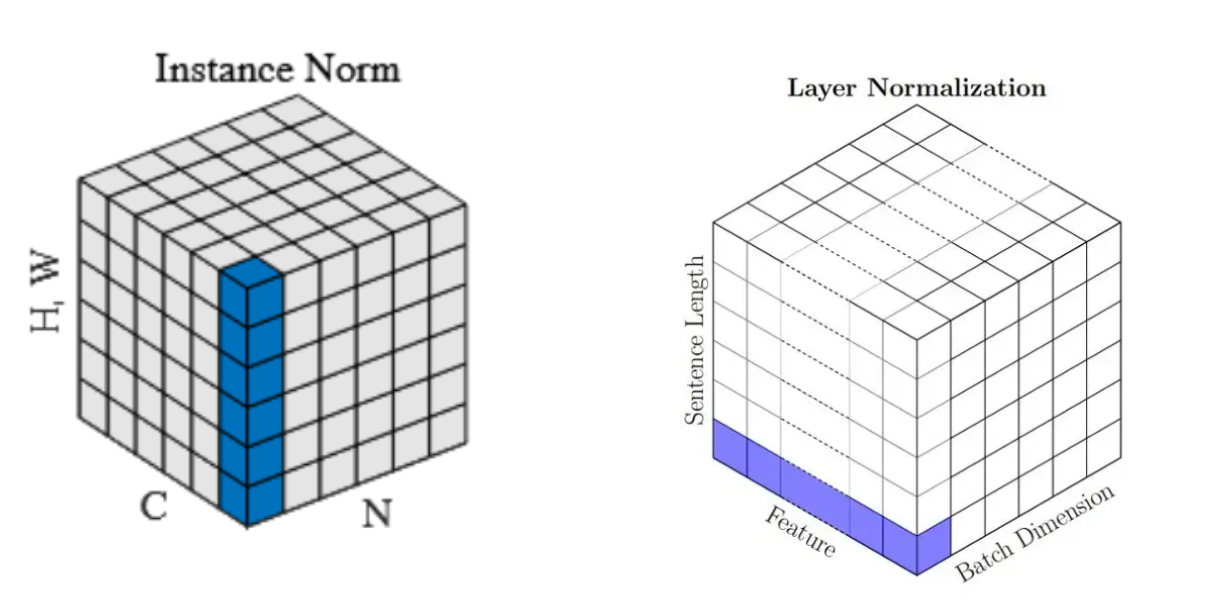InstanceNorm VS Transformer-LN

我们再来看一下Transformer-LayerNorm和CNN-InstanceNorm的图像区别，虽然他们看上去都是“一条”。但是作用域不同，所以含义不同。（反复强调）一个是横着的条，一个是竖着的条。

InstanceNorm我们之前已经解释过，它是将单个样本里的一个Channel进行Norm，是消除了每个通道内的统计偏差。通俗的说就是，对图像的一种特征（比如RGB通道里的蓝色）的图进行Norm。

Transformer下的LayerNorm的意思是就是将单个样本里的单个sequence的单个token的feature dimensions进行归一化，我么需要执行sequence x batch size次。也就是说，我们是对一个“字”的高维空间的相对向量进行Norm。

其实从含义上看，它确实很像InstanceNorm，专注于token本身，都是一种“自归一化”。这一步骤使得后续的自注意力层能更有效地计算不同Token之间的关系权重，最终促进模型构建出更加丰富和准确的上下文表示。

所以，从另一个层面，“动机”角度来说，IN旨在剥离实例级风格信息，而LN旨在稳定Token级特征表示，以服务于全局上下文的构建。

理论说完，我们看一下PyTorchInstanceNorm2d — PyTorch 2.7 documentation 中怎么说的。

PyTorch中IntanceNorm2d的解释

这里需要注意的是，PyTorch 将 IN的affine 默认为 False 是一个工程上的设计选择，可能基于在某些非风格迁移的生成任务（如某些GANs）中，禁用仿射变换能获得更稳定或更好的结果的考虑。而不是说理论领域的IN就没有仿射变换。

7.1.4 LayerNorm的代码实现

python

import torch
import torch.nn as nn

# 手动实现LayerNorm
class ManualLayerNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-5):
        super(ManualLayerNorm, self).__init__()
        if isinstance(normalized_shape, int):
            self.normalized_shape = (normalized_shape,)
        else:
            self.normalized_shape = tuple(normalized_shape)
        self.eps = eps
        self.gamma = nn.Parameter(torch.ones(self.normalized_shape))
        self.beta = nn.Parameter(torch.zeros(self.normalized_shape))
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        dims_to_normalize = tuple(range(x.ndim - len(self.normalized_shape), x.ndim))
        mean = x.mean(dim=dims_to_normalize, keepdim=True)
        var = x.var(dim=dims_to_normalize, unbiased=False, keepdim=True)
        x_normalized = (x - mean) / torch.sqrt(var + self.eps)
        output = self.gamma * x_normalized + self.beta
        return output
    

# 设置参数
batch_size = 4
seq_len = 10
embedding_dim = 32

# 创建一个随机输入张量
input_tensor = torch.randn(batch_size, seq_len, embedding_dim)

# 1. 初始化我们手动实现的 LayerNorm
manual_ln = ManualLayerNorm(normalized_shape=embedding_dim)

# 2. 初始化 PyTorch 内置的 LayerNorm
torch_ln = nn.LayerNorm(normalized_shape=embedding_dim)

# 分别计算输出
output_manual = manual_ln(input_tensor)
output_torch = torch_ln(input_tensor)

# 对比输出结果
print(f"手动实现的输出: {output_manual[0, 0, :10]}")
print(f"PyTorch 内置的输出: {output_torch[0, 0, :10]}")
print("-" * 30)

# 打印输出的形状
print(f"手动实现的输出形状: {output_manual.shape}")
print(f"PyTorch 内置的输出形状: {output_torch.shape}")
print("-" * 30)

# 验证两个输出是否非常接近
are_close = torch.allclose(output_manual, output_torch, atol=1e-6)

print(f"两个输出是否足够接近? {are_close}")

输出结果：

我们只查看一个，可以看出手动实现和torch自带的结果是一样的。并且我们通过allclose计算整体，得到了True

LayerNorm输出结果对比

7.2 RMSNorm

最后，RMSNorm，RMSNorm的公式和之前的Norm公式有很大的区别:

\begin{array}{r} RMSNorm (x) = γ ⊙ \frac{x}{RMS (x)} \\ RMS (x) = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} + ϵ} \end{array}

从公式上看，RMSNorm可以理解为LayerNorm的一个简化表示。也就是说：

RMSNorm的作用域和LayerNorm一样
RMSNorm比LayerNorm简单

既然作用域相同，那区别就是在简化步骤上了，RMSNorm为什么可以简化？为什么可以简化？

我们需要首先看看RMSNorm简化了什么。

7.2.1 RMSNorm对比LayerNorm简化内容

LayerNorm (x) = γ ⊙ \frac{x - μ}{\sqrt{σ^{2} + ϵ}} + β

这里面有四个核心操作：

计算均值 μ :中心化
计算方差 σ² (度量离散度)
应用增益 γ (重新缩放)
应用偏置 β (重新平移)

之前我们说过，在猜测BatchNorm等一系列Normalization为什么可以成功的时候，现在最主流的一个假设是“平滑损失曲面”，而这四个操作里，计算平均值用的第一个目的中心化明显不是，而方差是缩放的坟墓，分母和仿射变化的 $γ$ ，共同组成了重新缩放。而β是重新平移，FFN中也有这种偏置项，所以大概也不是重点。

那么重点就在“重新缩放”上了。分解一下：

RMSNorm没有 $μ$ ，也就是没有均值计算这一步。
因为没有均值，所以我们也没有办法计算方差。
原本的 $\sqrt{σ^{2} - ϵ}$ 则就替换为均方根，也就是 $\sqrt{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} + ϵ}$ 。
最后，在仿射变换方面，还没有 $β$ 。

但是还是不对啊，原始的transformer不是LayerNorm+ReLU么，ReLU这种非零均值的激活函数不是搭配LayerNorm这样包含中心化操作的才是比较稳定么？

在[[从激活函数到MOE]]中，曾经说过，部分场景下，激活函数的选择的一个动机是零均值，因为零均值的激活函数可以帮助我们加速梯度下降的收敛并稳定训练过程。传统的Transformer，ReLU不是零均值的，在工程上，LayerNorm的中心化操作在工程上帮助我们稳定了训练。

在RMSNorm中，去掉了中心化，这一操作理论上是反直觉的。因为其核心假设是LayerNorm的有效性主要来自重缩放不变性，而非中心化。为了证明这一点，RMSNorm+ReLU的组合也进行训练，实际结果证明，训练效率反而提升了。

这并不是说中心化不重要了，只是没我们原本想的那么重要。Transformer架构下，除了Norm我们还有残差连接稳定通路；训练过程中有Adam优化器；最关键的是，现代的Transformer架构的激活函数普遍选择GLU变体，这类函数因其门控结构，在处理来自前序归一化层的近零均值输入时，其输出本身即为“准零均值”。

简而言之吗，Norm中的中心化有用，但没有那么有用。从工程上看，去掉它的收益更大。

7.2.2 RMSNorm的代码实现

python

import torch
import torch.nn as nn


class ManualRMSNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-5):
        super().__init__()
        if isinstance(normalized_shape, int): self.normalized_shape = (normalized_shape,)
        else: self.normalized_shape = tuple(normalized_shape)
        self.eps = eps
        self.gamma = nn.Parameter(torch.ones(self.normalized_shape))
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        dims_to_normalize = tuple(range(x.ndim - len(self.normalized_shape), x.ndim))
        mean_squared = x.pow(2).mean(dim=dims_to_normalize, keepdim=True)
        rms = torch.sqrt(mean_squared + self.eps)
        return self.gamma * (x / rms)


# 设置参数
batch_size = 4
seq_len = 10
embedding_dim = 32

# 创建随机输入张量
input_tensor = torch.randn(batch_size, seq_len, embedding_dim)

# 1. 初始化我们手动实现的 RMSNorm
manual_rms = ManualRMSNorm(normalized_shape=embedding_dim)

# 2. 初始化 PyTorch 内置的 RMSNorm
torch_rms = nn.RMSNorm(normalized_shape=embedding_dim)

# 分别计算输出
output_manual = manual_rms(input_tensor)
output_torch = torch_rms(input_tensor)

# 对比输出结果
print(f"手动实现的输出: {output_manual[0, 0, :10]}")
print(f"PyTorch 内置的输出: {output_torch[0, 0, :10]}")
print("-" * 30)

# 打印输出的形状
print(f"手动实现的输出形状: {output_manual.shape}")
print(f"PyTorch 内置的输出形状: {output_torch.shape}")
print("-" * 30)

# 验证两个输出是否非常接近
are_close = torch.allclose(output_manual, output_torch, atol=1e-6)

print(f"两个输出是否足够接近? {are_close}")
max_diff = (output_manual - output_torch).abs().max().item()
print(f"两个输出之间的最大绝对差值: {max_diff}")

if are_close:
    print("\n验证成功！")
else:
    print("\n验证失败！")

得到结果：

RMSNorm输出结果对比

7.2.3 LayerNorm/RMSNorm在Transfomer中的代码

这里我们假设其Transfomer的其他模块都已经实现了，比如Attention和FFN

python

class TransformerEncoderBlock(nn.Module):
    def __init__(self, d_model: int, num_heads: int, d_ff: int, dropout: float = 0.1):
        super().__init__()
        self.self_attn = MultiHeadAttention(d_model, num_heads, dropout)
        self.feed_forward = PositionWiseFeedForward(d_model, d_ff, dropout)
        
        # 定义两个 LayerNorm/ 层。一个用于Attention一个用于FFN
        
        # self.norm1 = nn.LayerNorm(d_model)
        # self.norm2 = nn.LayerNorm(d_model)
        
        self.norm1 = nn.RMSNorm(d_model)
        self.norm2 = nn.RMSNorm(d_model)
		# 定义结束

        self.dropout1 = nn.Dropout(dropout)
        self.dropout2 = nn.Dropout(dropout)

    def forward(self, x: torch.Tensor, mask=None) -> torch.Tensor:
        # --- 第一个子层：多头自注意力 + Add & Norm ---
        attn_output = self.self_attn(q=x, k=x, v=x, mask=mask)
        # 2. Add & Norm
        #    Add: 残差连接 (x + dropout(attn_output))
        #    Norm: Layer Normalization
        x = self.norm1(x + self.dropout1(attn_output))
        
        # --- 第二个子层：前馈网络 + Add & Norm ---
        # 1. 计算前馈网络
        ff_output = self.feed_forward(x)
        # 2. Add & Norm
        #    Add: 残差连接 (x + dropout(ff_output))
        #    Norm: Layer Normalization
        x = self.norm2(x + self.dropout2(ff_output))
        
        return x

8 结语

写到这片的时候，其实已经开始考验很多前置知识了。所以我想要既要入门友好又要写的全面深入（既要又要），确实很磨时间，当然更主要的原因是上班实在是太耽误写东西了。

这里没有讨论Pre-Norm和Post-Norm，后续会出一篇（争取短一点）的来说明。

代码依旧在Google Colab： https://colab.research.google.com/drive/1OWxUBZm_hIx28S4y278yXGIfnfcdUDXg?usp=drive_link

https://colab.research.google.com/drive/1D-8FcyDknUDdwSMFXkIGEI80ebqYeHTd?usp=drive_link

示意图在： https://demo.phimes.top/?page=embedding

9 引用

Ba, J. L., Kiros, J. R., & Hinton, G. E. (2016). Layer Normalization. arXiv. https://doi.org/10.48550/arXiv.1607.06450
Bjorck, J., Gomes, C., Selman, B., & Weinberger, K. Q. (2018). Understanding Batch Normalization. arXiv. https://doi.org/10.48550/arXiv.1806.02375
Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2021). An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv. https://doi.org/10.48550/arXiv.2010.11929
Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv. https://doi.org/10.48550/arXiv.1502.03167
Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin, S., & Guo, B. (2021). Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv. https://doi.org/10.48550/arXiv.2103.14030
PRIMO.ai. (n.d.). Manifold Hypothesis. Retrieved July 29, 2025, from https://primo.ai/index.php?title=Manifold_Hypothesis
PyTorch. (n.d.-a). InstanceNorm2d. PyTorch 2.7 documentation. Retrieved July 29, 2025, from https://pytorch.ac.cn/docs/stable/generated/torch.nn.InstanceNorm2d.html
PyTorch. (n.d.-b). LayerNorm. PyTorch 2.7 documentation. Retrieved July 29, 2025, from https://pytorch.ac.cn/docs/stable/generated/torch.nn.LayerNorm.html
Santurkar, S., Tsipras, D., Ilyas, A., & Madry, A. (2019). How Does Batch Normalization Help Optimization? arXiv. https://doi.org/10.48550/arXiv.1805.11604
Shen, S., Yao, Z., Gholami, A., Mahoney, M. W., & Keutzer, K. (2020). PowerNorm: Rethinking Batch Normalization in Transformers. arXiv. https://doi.org/10.48550/arXiv.2003.07845
Singh, A. (2024, August 13). Unpacking Word Embeddings: A Journey Through Modern NLP Techniques. Medium. https://medium.com/@aashish.singh2k8/unpacking-word-embeddings-a-journey-through-modern-nlp-techniques-8a2ca21f1e46
Ulyanov, D., Vedaldi, A., & Lempitsky, V. (2017). Instance Normalization: The Missing Ingredient for Fast Stylization. arXiv. https://doi.org/10.48550/arXiv.1607.08022
Wu, Y., & He, K. (2018). Group Normalization. arXiv. https://doi.org/10.48550/arXiv.1803.08494
Xie, Q., Dai, Z., Hovy, E., Luong, M.-T., & Le, Q. V. (2019). Unsupervised Data Augmentation for Consistency Training. arXiv. https://doi.org/10.48550/arXiv.1904.12848
Yin, P., Dong, Q., Kumar, A., & Van Durme, B. (2020). On the Generalization Effects of Linear Transformations in Data Augmentation. arXiv. https://doi.org/10.48550/arXiv.2005.00695
YOLOv4 P7. (n.d.). 词嵌入（Word Embedding）. IBM. Retrieved July 29, 2025, from https://www.ibm.com/cn-zh/think/topics/word-embeddings
代码诗人. (2023, December 26). 深入探讨Word Embedding：从Word2Vec到BERT，揭示词向量的奥秘. 稀土掘金. https://juejin.cn/post/7317703203633332251
储泉. (2024, October 15). NLP 中的词向量（一）：词的表示. 储泉的博客. https://chuquan.me/2024/10/15/nlp-word-representation/

Add & Norm（二）：从传统CV到Transformer里的Normalizaiton详解

作者phimes

发布于2025/7/28

更新于今日内

许可协议 CC BY-NC-SA 4.0

署名-非商业性使用-相同方式共享 4.0 国际

LLM 算法原理

反馈与投诉

Add & Norm（二）：从传统CV到Transformer里的Normalizaiton详解

1 写在前面 ​

1.1 TL;DR ​

2 Normalization的定义 ​

3 Norm的动机 ​

3.1 中心协变量偏移 ​

3.2 平滑损失曲面 ​

4 不同的领域的数据 ​

4.1 传统CV下的数据样式 ​

4.1.1 空间结构性 ​

4.1.2 平移不变性 ​

4.1.3 通道相关性 ​

4.2 NLP下的数据样式 ​

4.3 NLP和CNN数据在空间上的转换 ​

5 Normalization ​

5.1 CNN中的Norm ​

5.1.1 Batch Norm ​

5.1.1.1 定义 ​

5.1.1.2 公式 ​

5.1.1.3 BN示意图 ​

5.1.1.4 理解BatchNorm的隐式表达 ​

5.1.1.5 仿射变换 ​

5.1.1.6 对比torch实现和手动实现BN ​

5.1.2 Layer Norm ​

5.1.2.1 定义 ​

5.1.2.2 公式 ​

5.1.2.3 CNN-LN示例图 ​

5.1.2.4 理解CNN-LN的隐式表达 ​

5.1.3 InstanceNorm ​

5.1.3.1 定义 ​

5.1.3.2 公式 ​

5.1.3.3 理解IN的隐式表达 ​

5.1.4 Group Norm/Power Norm ​

5.1.4.1 定义 ​

5.1.4.2 公式 ​

5.1.4.3 理解GN的隐式表达 ​

6 看了这么多，Normalization的本质是？ ​

7 在Transformer中的Normalization ​

7.1 LayerNorm ​

7.1.1 数据形态及其特点 ​

7.1.2 “层”概念的不同 ​

7.1.3 Transformer中的LayerNorm的可视化 ​

7.1.4 LayerNorm和InstanceNorm的区别 ​

7.1.4 LayerNorm的代码实现 ​

7.2 RMSNorm ​

7.2.1 RMSNorm对比LayerNorm简化内容 ​

7.2.2 RMSNorm的代码实现 ​

7.2.3 LayerNorm/RMSNorm在Transfomer中的代码 ​

8 结语 ​

9 引用 ​

1 写在前面

1.1 TL;DR

2 Normalization的定义

3 Norm的动机

3.1 中心协变量偏移

3.2 平滑损失曲面

4 不同的领域的数据

4.1 传统CV下的数据样式

4.1.1 空间结构性

4.1.2 平移不变性

4.1.3 通道相关性

4.2 NLP下的数据样式

4.3 NLP和CNN数据在空间上的转换

5 Normalization

5.1 CNN中的Norm

5.1.1 Batch Norm

5.1.1.1 定义

5.1.1.2 公式

5.1.1.3 BN示意图

5.1.1.4 理解BatchNorm的隐式表达

5.1.1.5 仿射变换

5.1.1.6 对比torch实现和手动实现BN

5.1.2 Layer Norm

5.1.2.1 定义

5.1.2.2 公式

5.1.2.3 CNN-LN示例图

5.1.2.4 理解CNN-LN的隐式表达

5.1.3 InstanceNorm

5.1.3.1 定义

5.1.3.2 公式

5.1.3.3 理解IN的隐式表达

5.1.4 Group Norm/Power Norm

5.1.4.1 定义

5.1.4.2 公式

5.1.4.3 理解GN的隐式表达

6 看了这么多，Normalization的本质是？

7 在Transformer中的Normalization

7.1 LayerNorm

7.1.1 数据形态及其特点

7.1.2 “层”概念的不同

7.1.3 Transformer中的LayerNorm的可视化

7.1.4 LayerNorm和InstanceNorm的区别

7.1.4 LayerNorm的代码实现

7.2 RMSNorm

7.2.1 RMSNorm对比LayerNorm简化内容

7.2.2 RMSNorm的代码实现

7.2.3 LayerNorm/RMSNorm在Transfomer中的代码

8 结语

9 引用